My Research 研究紹介
時系列信号からのパラメータ空間の推定(分岐図再構成)
異なるパラメータを用いて作成した複数の時系列信号のみから対象の系のパラメータ空間を推定し,推定したパラメータ空間上でのダイナミクス解析を行う.
本研究の条件は,パラメータの次元や値などの情報は未知であり,単一のシステムから異なるパラメータで生成された時系列信号のみを使用する.本研究の概要を図1 に示す.
本研究の先行研究は,1994 年にTokunaga らにより発表された時系列信号のみからの分岐図再構成[1] である.
近年,IoT デバイスやウェアラブル端末としてセンサー技術が発展し観測できる時系列信号は多岐に渡っている.
この観測した時系列信号のみからパラメータ空間を推定し,パラメータが変化したときの時系列信号の推定と,そのダイナミクスが解析できれば,系の制御や予測などの応用が期待できる.
他にも,生体信号などの測定回数が限られるデータに適用すれば,少ない計測データでパラメータが変化した時の信号の振舞を推定し,薬を使った適切な治療が期待できる.
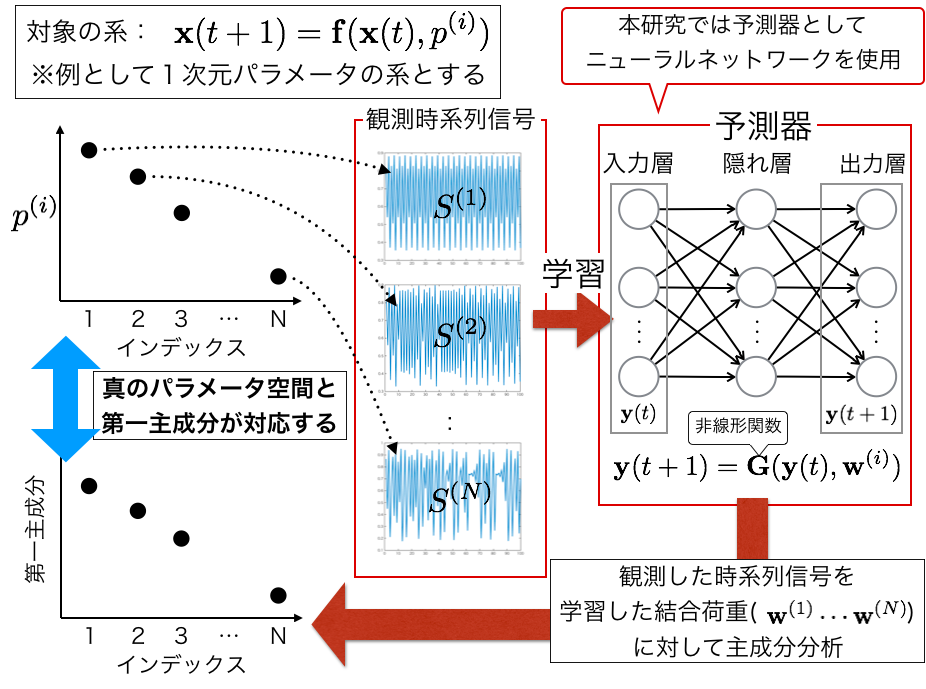
図1 本研究の概要
[1] Tokunaga et al., Reconstructing bifurcation diagrams only from time-waveforms, Physica D, No.79, 1994
分岐図とは?
分岐図とは,分岐現象(パラメータが変わったときの状態値の振舞いの変化)をプロットした図である.一次元パラメータの系の場合,横軸にパラメータ値,縦軸に状態値をプロットする.
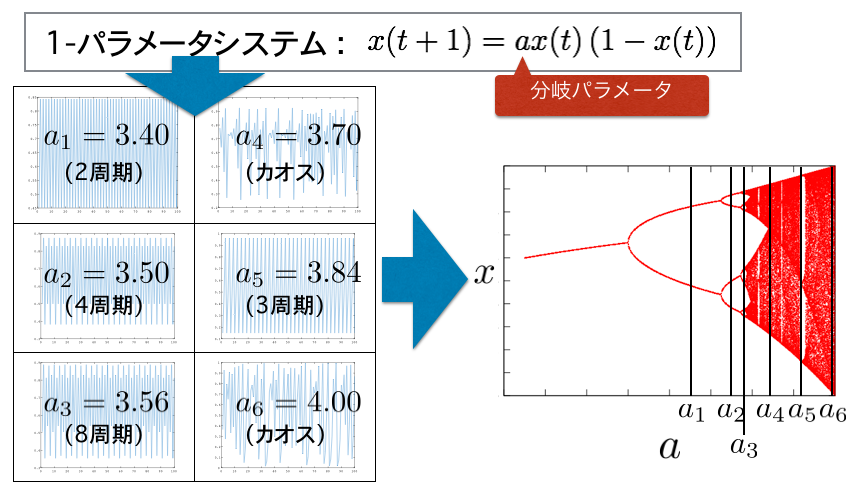
図2 分岐図
※a=3.40では2周期振動のため分岐図上では2点プロットされる
※a=3.50では4周期振動のため分岐図上では4点プロットされる
※a=3.56では8周期振動のため分岐図上では8点プロットされる
※a=3.70ではカオス振動のため分岐図上では様々な点がプロットされる
分岐図再構成とは?
対象の系は未知とし,複数の時系列信号のみが与えられた状態で分岐図を再構成する.
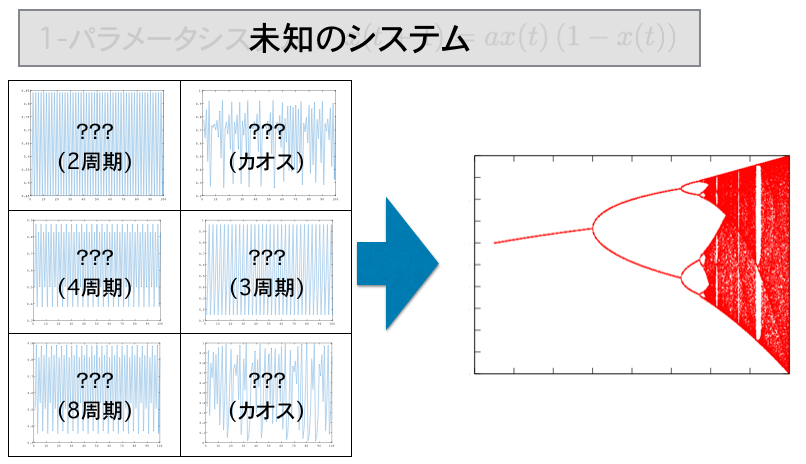
図3 分岐図再構成
